Wektory dystrybucyjne: przestrzeń wektorów dystrybucyjnych i statyczne wektory dystrybucyjne

Zadbaj o dobrą organizację dzięki kolekcji Zapisuj i kategoryzuj treści zgodnie ze swoimi preferencjami.

Wektor dystrybucyjny jest wektorową reprezentacją danych w przestrzeni wektorów dystrybucyjnych. Ogólnie mówiąc, model znajduje potencjalne wektory dystrybucyjne za pomocą projekcji wielowymiarowej przestrzeni początkowych wektorów danych na przestrzeń o mniejszej liczbie wymiarów. Porównanie danych w przestrzeni wielowymiarowej z tymi w przestrzeni o mniejszej liczbie wymiarów znajdziesz w module Dane kategorialne.

Wektory dystrybucyjne ułatwiają uczenie maszynowe na dużych wektorach cech, takich jak rozproszone wektory reprezentujące artykuły żywnościowe omówione w poprzedniej sekcji. Względne pozycje elementów w przestrzeni wektorów dystrybucyjnych niekiedy mają potencjalne powiązanie semantyczne, ale proces znajdowania przestrzeni o mniejszej liczbie wymiarów i względnych pozycji w tej przestrzeni często nie jest możliwy do zinterpretowania przez człowieka, a wynikowe wektory dystrybucyjne są trudne do zrozumienia.

Aby zrozumieć, jak wektory dystrybucyjne reprezentują informacje, przyjrzyj się tej jednowymiarowej reprezentacji dań takich jak hot dog, pizza, sałatka, szawarma i barszcz na skali od „najmniej podobnych do kanapki” do „najbardziej podobnych do kanapki”. Pojedynczy wymiar to urojona miara „kanapkowości”.

Gdzie na tej linii powinien znajdować się strudel jabłkowy? Można przypuszczać, że gdzieś między pozycjami hot dog i shawarma. Strudel jabłkowy ma też jednak inny wymiar – słodkość lub deserowość, a to wyraźnie odróżnia go od pozostałych elementów. Odzwierciedla to poniższy rysunek, na którym dodano wymiar „deserowość”:

Wektor dystrybucyjny reprezentuje każdy element w n-wymiarowej przestrzeni za pomocą n liczb zmiennoprzecinkowych (zazwyczaj w zakresie od –1 do 1 lub od 0 do 1). Na rysunku 3 każdą potrawę reprezentuje wektor dystrybucyjny w przestrzeni jednowymiarowej z 1 współrzędną, a na rysunku 4 – w przestrzeni dwuwymiarowej z 2 współrzędnymi. Na rysunku 4 „strudel jabłkowy” znajduje się w prawym górnym kwadrancie wykresu i można do niego przypisać punkt (0,5, 0,3), a „hot dog” znajduje się w prawym dolnym kwadrancie wykresu i można do niego przypisać punkt (0,2, –0,5).

W przestrzeni wektorów dystrybucyjnych odległość między dowolnymi 2 elementami można obliczyć matematycznie i zinterpretować jako miarę względnego podobieństwa między nimi. 2 rzeczy, które są blisko siebie, np. shawarma i hot dog na rysunku 4, są bliżej ze sobą powiązane w reprezentacji danych modelu niż 2 rzeczy bardziej od siebie oddalone, takie jak apple strudel i borscht.

Zauważ też, że w przestrzeni 2D na rysunku 4 element apple strudel jest znacznie bardziej oddalony od shawarma i hot dog, niż miałoby to miejsce w przestrzeni 1D. Jest to zgodne z intuicją – element apple strudel nie jest tak podobny do hot doga czy szawarmy jak hot dog i shawarma są podobne do siebie.

Spójrzmy teraz na barszcz. To potrawa znacznie bardziej płynna niż pozostałe. Potrzebujemy więc kolejnego wymiaru – płynności, będącego miarą tego, jak bardzo płynna może być potrawa. Po dodaniu tego wymiaru elementy można zwizualizować w 3D w ten sposób:

Gdzie w tej przestrzeni 3D umieścić chiński deser tangyuan? Przypomina on zarówno zupę taką jak barszcz, jak i słodki deser taki jak strudel jabłkowy. Zdecydowanie różni się od kanapki. Oto możliwa lokalizacja:

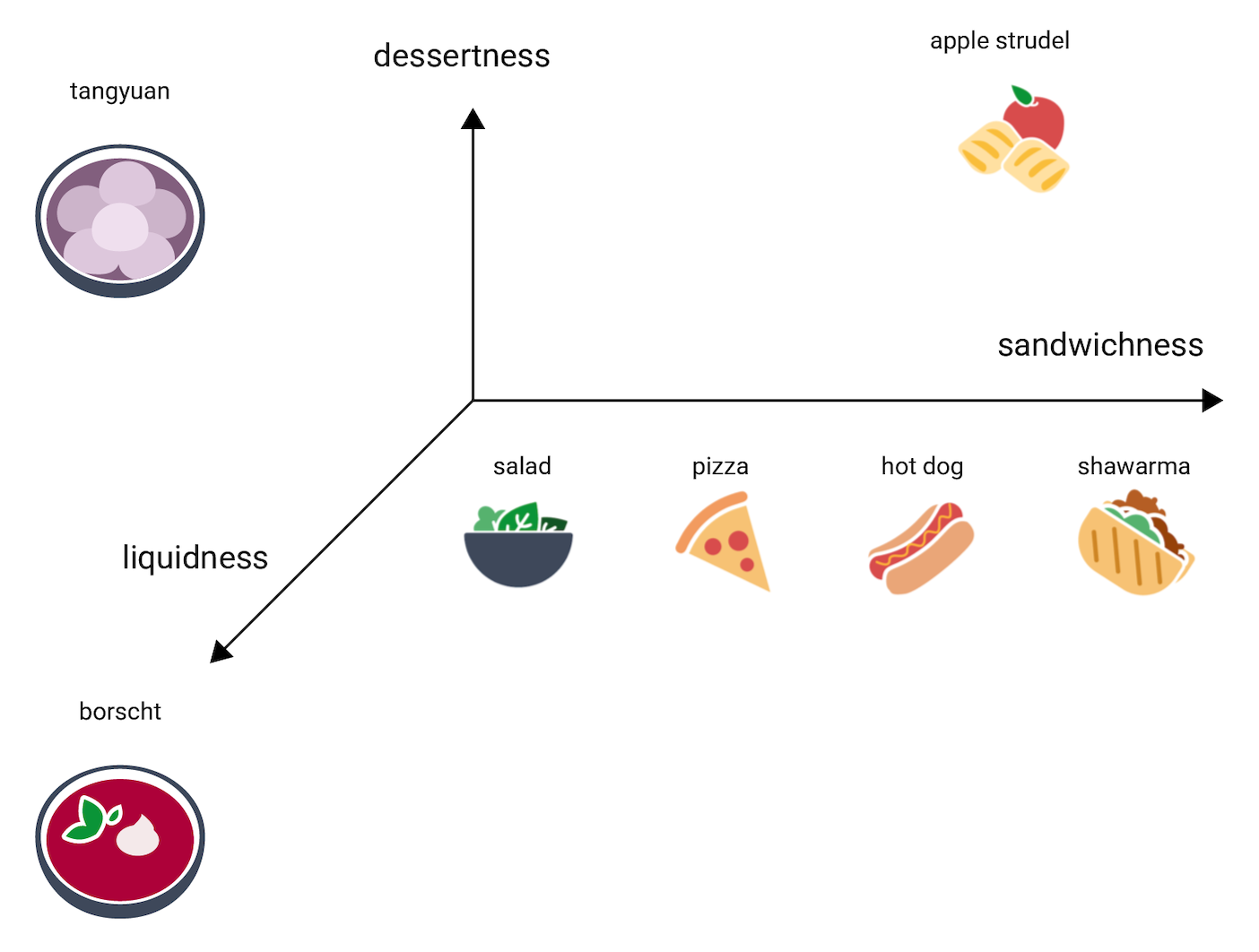
Zauważ, jak dużo informacji pokazują te wykresy. Można sobie wyobrazić dodanie kolejnych wymiarów, wskazujących na przykład, jak bardzo mięsna lub pieczona jest potrawa. Przestrzenie 4D, 5D i te z jeszcze większą liczbą wymiarów trudno jednak zwizualizować.

Przestrzenie wektorów dystrybucyjnych w świecie rzeczywistym

W świecie rzeczywistym przestrzenie wektorów dystrybucyjnych są d-wymiarowe, gdzie d to znacznie więcej niż 3, jednak mniej niż wymiarowość danych. Powiązania między punktami danych nie zawsze są tak intuicyjne jak w powyższym fikcyjnym przykładzie. (W przypadku wektorów dystrybucyjnych słowa wartość d to często 256, 512 lub 1024)¹.

W praktyce osoba konfigurująca ML zazwyczaj ustawia konkretne zadanie i liczbę wymiarów przestrzeni wektorów dystrybucyjnych. Następnie model próbuje rozmieścić przykłady treningowe tak, aby znajdowały się blisko siebie w przestrzeni wektorów dystrybucyjnych z określoną liczbą wymiarów, lub dostraja się do liczby wymiarów, jeśli wartość d nie jest ustalona. Poszczególne wymiary rzadko są tak zrozumiałe jak „deserowość” czy „płynność”. Niekiedy ich „znaczenie” można wywnioskować, ale nie zawsze jest to możliwe.

Wektory dystrybucyjne zazwyczaj są dostosowane do konkretnego zadania i różnią się między różnymi zadaniami. Na przykład wektory dystrybucyjne, które wygenerował model klasyfikujący potrawy według kategorii wegetariańskie – niewegetariańskie, będą inne niż wektory dystrybucyjne wygenerowane przez model sugerujący potrawy na podstawie pory dnia lub pory roku. Na przykład „płatki zbożowe” i „kiełbaska śniadaniowa” prawdopodobnie będą bliżej siebie w przestrzeni wektorów dystrybucyjnych w modelu uwzględniającym porę dnia, ale daleko od siebie w modelu rozróżniającym potrawy wegetariańskie i niewegetariańskie.

Statyczne wektory dystrybucyjne

W różnych zadaniach wektory dystrybucyjne są różne, ale pojedyncze zadanie ma pewien ogólny cel – przewidywanie kontekstu słowa. Modele trenowane do przewidywania kontekstu słowa zakładają, że słowa pojawiające się w podobnych kontekstach są powiązane semantycznie. Na przykład dane treningowe zawierające zdania „Zjechali do Wielkiego Kanionu na ośle” i „Zjechali do kanionu na koniu” sugerują, że słowa „koniu” i „ośle” pojawiają się w podobnych kontekstach. Okazuje się, że wektory dystrybucyjne oparte na podobieństwie semantycznym świetnie sprawdzają się w wielu ogólnych zadaniach językowych.

Dobrym przykładem, mimo że jest starszy i w znacznej mierze został zastąpiony przez inne modele, jest model word2vec. Model word2vec jest trenowany na korpusie dokumentów w celu uzyskania 1 globalnego wektora dystrybucyjnego na słowo. Gdy każde słowo lub każdy punkt danych ma pojedynczy wektor dystrybucyjny, jest on nazywany statycznym wektorem dystrybucyjnym. Trenowanie modelu word2vec pokazano w uproszczeniu na poniższym filmie.

Badania sugerują, że te statyczne wektory dystrybucyjne po wytrenowaniu mają do pewnego stopnia zakodowane informacje semantyczne, zwłaszcza w powiązaniach między słowami. Oznacza to, że słowa, które są używane w podobnych kontekstach, w przestrzeni wektorów dystrybucyjnych są bliżej siebie. To, jakie konkretnie wektory dystrybucyjne zostaną wygenerowane, zależy od korpusu użytego do trenowania. Więcej informacji (w języku angielskim): T. Mikolov et al (2013), „Efficient estimation of word representations in vector space” (Efektywna ocena reprezentacji słów w przestrzeni wektorowej).